Dopplereffect

Wat onderzoeken we?

Wij, Julian en Jerke, onderzoeken het dopplereffect. We verplaatsen een geluidsbron met een hoge snelheid langs een microfoon en bekijken de frequentie voor en na het passeren van de geluidsbron. We vergelijken dit dan met de verwachte waarden.
-Jerke Ghekiere

Dopplereffect

Dopplereffect.

1. Inhoudstafel

1. Inhoudstafel
2. Geschiedenis
3. Beschrijving Dopplereffect
4. Toepassingen
4.1 De doppler
4.2 Radartechnologie
4.3 Debietmetingen
5. Wiskunde
6. Proef
6.1 Idee
6.2 Keuze voortuig
6.3 Doel
6.4 Resultaten
6.5 Verwerking
Download PDF

2. Geschiedenis

Het Dopplereffect, genoemd naar de Oostenrijkse wetenschapper Christian

Doppler, is een fenomeen dat zowel bij geluidsgolven als bij lichtgolven waar te nemen is. Rond 1840 ontdekten astronomen dat sterren verschillende kleuren licht uitstralen, maar de oorzaak van deze variatie was toen nog onbekend. Doppler voerde onderzoek uit naar dubbelsterren, twee sterren die om elkaar draaien, en veronderstelde dat het kleurverschil werd veroorzaakt door de relatieve beweging van de sterren ten opzichte van de aarde. Hij presenteerde zijn theorie in 1842, waarbij hij beweerde dat dit effect zowel voor geluids- als voor lichtgolven gold, waarbij bij geluid de toon verandert en bij licht de kleur.

Deze hypothese werd echter met scepsis ontvangen. In een poging om het Dopplereffect te weerleggen, voerde de Nederlandse wetenschapper Christophorus Buys Ballot in 1845 een experiment uit. Hij liet een locomotief met hoornisten op een platte wagon rijden op het spoor tussen Maarssen en Utrecht om metingen te verrichten. De resultaten bevestigden Dopplers theorie, en zo werd het Dopplereffect voor het eerst experimenteel bewezen.

Ondanks deze bevestiging bleef er twijfel bestaan over de toepasbaarheid van het Dopplereffect op astronomische waarnemingen. Dit kwam voort uit Dopplers aanname dat alle sterren wit licht uitstralen, wat betekende dat de kleuren die we waarnemen alleen het gevolg zijn van hun relatieve beweging ten opzichte van de aarde. Hoewel deze aanname later onjuist bleek te zijn, bleef het Dopplereffect zelf een essentieel concept in zowel de astronomie als de natuurkunde, waarbij het begrip van bewegende licht- en geluidsbronnen werd verklaard.

3. Beschrijving Dopplereffect

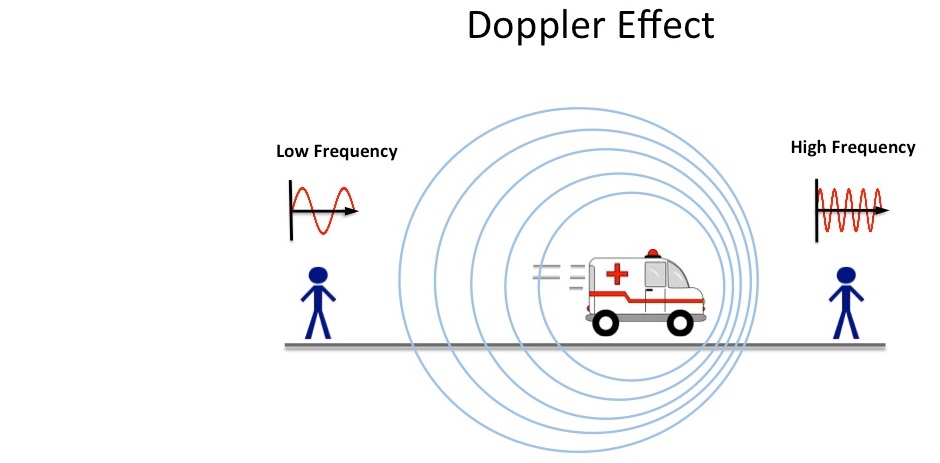
Het Dopplereffect omvat de verandering in frequentie van een golf. Deze verandering kan worden waargenomen door een waarnemer die relatief in beweging is ten opzichte van de bron van de golf. Met dit effect komen we in het dagelijks leven veel in contact.

Een van de bekendste voorbeelden is de verandering in toonhoogte van een sirene van een ambulance die nadert en vervolgens voorbijrijdt. Wanneer de sirene nadert, worden de geluidsgolven samengedrukt, dit resulteert in een hogere frequentie en dus ook een hogere toon. Omgekeerd, als de sirene weg beweegt, worden de geluidsgolven uitgerekt, wat resulteert in een lagere frequentie. Het Dopplereffect wordt veroorzaakt doordat de bron en ontvanger van het geluid ten opzichte van elkaar bewegen. Hij presenteerde zijn theorie in 1842, waarbij hij beweerde dat dit effect zowel voor geluids- als voor lichtgolven gold, waarbij bij geluid de toon verandert en bij licht de kleur.

Het gebeurt met geluid omdat geluid uit golven bestaat die zich met een vaste snelheid voortplanten, maar dit effect geldt ook voor elektromagnetische straling zoals licht. Omdat licht bestaat uit golven die zich ook met een vaste snelheid voorplanten, kan het Dopplereffect ook optreden. Het resultaat hiervan is dat je een rood- of blauwverschuiving van het licht krijgt.

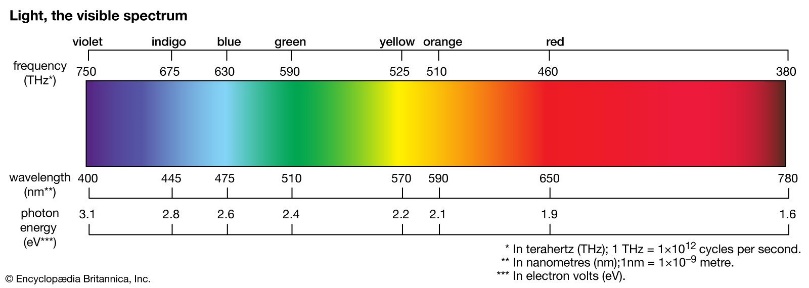
Wanneer een lichtbron naar je toe of weg van je beweegt met een bepaalde snelheid, dan zal het licht dat uitgezonden is door de bron een andere kleur hebben dan het licht dat je waarneemt. Bij kleine snelheden is dit minimaal, maar bijvoorbeeld bij sterren die een grote snelheid hebben, is de verandering duidelijker. Als zo’n ster naar ons toe beweegt, dan zal de frequentie van de lichtgolf vermeerderen. Op een lichtspectrogram kan je zien dat grotere frequenties naderen naar het blauwe deel van het spectrum, daarom noemen ze dat blauwverschuiving.

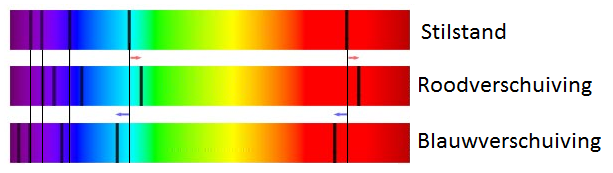
Omgekeerd heb je ook roodverschuiving, dit komt dan voor als een ster van je weg beweegt. Het effect is weliswaar te klein om er in het dagelijks leven iets van te merken in het volledig lichtspectrum, dat we ontvangen. Door metingen uit te voeren kunnen we de rood- en blauwverschuiving wel visueel voorstellen. Het effect wordt bijvoorbeeld gebruikt om te meten als sterren naar ons toe bewegen of van ons wegtrekken. Op het spectrum kunnen we dit waarnemen door de verschuiving van de absorptielijnen (zie onderstaande afbeelding).

4. Toepassingen

4.1 De doppler

Een belangrijke toepassing van het Dopplereffect is de doppler. Dit is een apparaatje waarmee je naar het hart van een ongeboren baby kan luisteren. Hierbij worden geluidsgolven uitgezonden door het apparaatje en botsen deze golven tegen de trillingen van de bloedsomloop van de foetus zelf. De teruggekaatste golven neemt het dopplerapparaat terug op, het apparaat kan deze gegevens hoor- en zichtbaar maken. Op basis van het gemeten frequentieverschil van uitgestraalde en teruggekaatste golf wordt de snelheid en de richting van het bloed bepaald.

4.2 Radartechnologie

Het Dopplereffect wordt ook gebruikt in radartechnologie. Er worden radiogolven met een bepaalde frequentie uitgestuurd. Wanneer die een object tegenkomen, zullen de radiogolven terugkaatsen met een andere frequentie. Een sensor in de radar meet het verschil in de frequenties. Daaruit kan je dan de snelheid bepalen van het object. Radartechnologie wordt gebruikt om de snelheid, grootte en richting van een vliegtuig te bepalen. Maar deze technologie kan ook gebruikt worden voor het berekenen van de snelheid van een wagen. Hierbij wordt een snelheidsmeter gebruikt die je richt op een voertuig.

Met de formule \(v = (\frac{\Delta f}{f})(\frac{c}{2})\) kunnen we dan de snelheid van de wagen berekenen.

In deze formule is:

\(v =\) de snelheid van het voertuig

\(\Delta f = \) het verschil in de frequentie tussen de uitgezonden golven en teruggekaatste golven.

\(f =\) de uitgezonden frequentie

\(c =\) de lichtsnelheid (299 792 458m/s)

Rekenvoorbeeld:

Stel dat we een Pocket Radar gebruiken als snelheidsmeter. Dit toestel heeft een frequentie van 24,125 GHz. Stel hierbij ook dat het verschil in frequentie tussen de uitgezonden en de teruggekaatste golf 5 KHz is. Uit bovenstaande formule kunnen we dan de snelheid van het voertuig berekenen.

\(v(\frac{m}{s}) = (\frac{5\cdot 10^{3}}{24,125\cdot 10^{9}})(\frac{299.792.458}{2}) = 31,06 m/s\)

\(v(\frac{km}{h}) = 31,06\cdot 3.6 = 111,84km/h\)

4.3 Debietmetingen

Bij debietmetingen verzendt de waarnemer geluidsgolven. Deze golven hebben hun eigen frequentie die wijzigt wanneer ze teruggekaatst worden na een botsing met een stromende stof. Men stelt vast dat er een lineair verband is tussen de frequentieverschuiving en de snelheid van de stof. Met dit verband kan men het debiet bepalen.

5. Wiskunde

Geluidsbron in rust

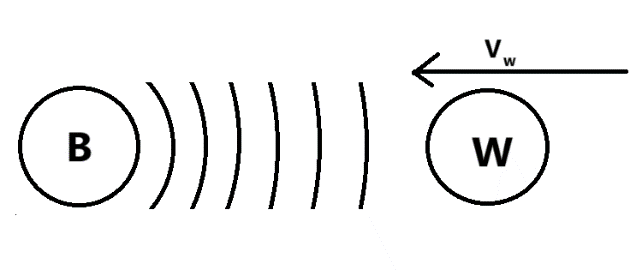
De waarnemer beweegt naar een bron toe en brengt daarbij een geluid voort met een frequentie f. Hierbij is zijn snelheid gelijk aan \(v_{w}\) in m/s. Indien 𝑣 de voortplantingssnelheid van het geluid voorstelt, dan is de golflengte λ en de frequentie f te noteren als:

\(\lambda = \frac {v}{f}\)

\(f = \frac {v}{\lambda}\)

Doordat de waarnemer beweegt ten opzichte van de bron moet men de voortplantingssnelheid beschouwen als \((v+v_{w})\). Hierdoor wordt de waargenomen frequentie 𝑓′ als volgt gedefinieerd:

\(f' = \frac{v+v_{w}}{\lambda} = \frac{v+v_{w}}{\frac{v}{f}} = f\frac{v+v_{w}}{v}\)

Als de waarnemer nadert, wordt de waargenomen frequentie dus telkens groter dan de werkelijke frequentie van de bron. Hierdoor hoort men dus een hogere toon dan de werkelijke.

Als de waarnemer zich verwijdert van de bron, wordt in bovenstaande formule het plusteken vervangen door een minteken. In dit geval is de waargenomen frequentie kleiner dan de werkelijke frequentie van de bron. Hierdoor hoort men een toon die lager is dan die uitgezonden door de geluidsbron.

De algemene formule voor waarnemer in beweging is dus:

\(f' = f\frac {v\pm v_{w}}{v}\) (+ = naar elkaar toe, - = van elkaar weg)

Geluidsbron in beweging

We veronderstellen nu dat een geluidsbron wel nadert ten opzichte van een stilstaande waarnemer met een snelheid van \(v_{b}\). Hierbij stellen we de oorspronkelijke afstand tussen waarnemer W en geluidsbron B gelijk aan s. Na \(t_{1}\) seconden bereikt het eerste golffront het oor van de waarnemer.

\(t_{1} = \frac {s}{v}\)

Wanneer de bron zich nu verplaatst, zendt hij na T seconden een tweede golffront uit. Het golffront bereikt de waarnemer na \(t_{2}\) seconden:

\(t_{2} = T + \frac {s-v_{b}T}{v}\)

Met bovenstaande uitdrukking voor 𝑡1 en 𝑡2 kunnen we het tijdsverschil Δt berekenen tussen het aankomen van het eerste golffront en het tweede golffront:

\(\Delta t = T + \frac{s-v_{b}T}{v} - \frac{s}{v} = T - \frac{v_{b}T}{v} = T(\frac{v-v_{b}}{v})\)

De waargenomen frequentie is gelijk aan het omgekeerde van dit tijdsverschil. Hieruit kunnen we stellen dat:

\(f' = f(\frac {v}{v-v_{b}})\)

Uit bovenstaande formule kan je afleiden dat wanneer de waarnemer naar de bron toe beweegt de gehoorde toon hoger is dan de werkelijke toon. Als de waarnemer zich wegtrekt van de bron is de gehoorde toon lager dan de werkelijke toon.

Algemeen kunnen we de formule voor de waargenomen frequentie bij een waarnemer en een bron in beweging noteren als:

\(f' = f(\frac {v \pm v_{w}}{v \pm v_{b}})\)

(+ in de teller, - in de noemer = naar elkaar toe)

(- in de teller, + in de noemer = van elkaar weg)

6. Proef

6.1 Idee

Ons idee is om een wagentje te verplaatsen met een constante snelheid. Op dit wagentje zal een geluidsbron staan die een bepaalde frequentie zal uitzenden. Wanneer dit wagentje naar de geluidssensor toe verplaatst, zal de waargenomen frequentie groter zijn dan de uitgezonden frequentie en omgekeerd. Dit wagentje zal worden voortgetrokken door een motor.

6.2 Keuze voertuig

We hebben ervoor gekozen om het wagentje te verplaatsen door eraan te trekken in plaats van het automatisch te laten rijden, omdat er dan minder gewicht moet verplaatst worden. Bovendien kan een externe motor een grotere snelheid bereiken. En hoe groter de snelheid, hoe groter het verschil in frequentie.

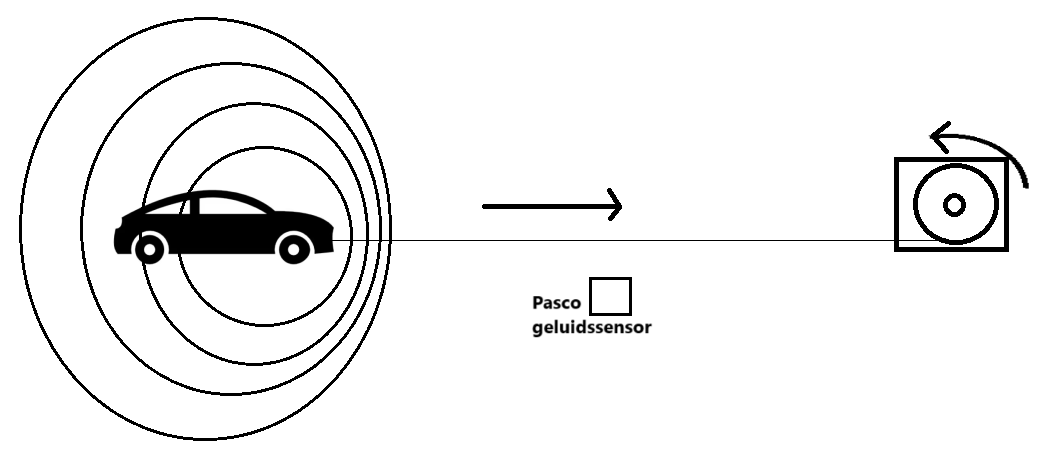
6.3 Doel

Het doel van onze proef is om het Dopplereffect waar te nemen voor een voertuig dat zich met een constante snelheid verplaatst ten opzichte van een stilstaande waarnemer. Dus we willen aantonen dat de frequentie verhoogt als het voertuig nadert en verlaagt wanneer het voertuig wegtrekt.

6.4 Resultaten

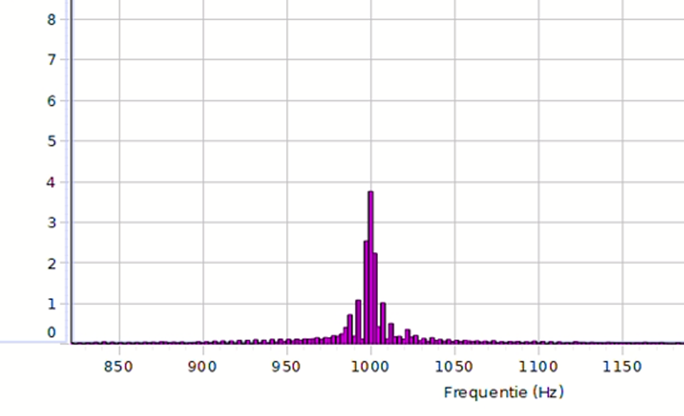
De grafieken stellen de geluidssterkte in functie van de frequentie voor.

Grafiek 1: Het wagentje is in rust op ongeveer 8 meter van de geluidssensor.

We kunnen zien op de grafiek dat er een frequentie uitgezonden wordt van 1000 Hz.

Grafiek 2: Het wagentje beweegt naar de geluidssensor toe.

We zien dat er nu een frequentie van ongeveer 1020 Hz gemeten wordt.

Grafiek 3: Het wagentje is net voorbij de sensor.

Grafiek 5: Het wagentje is opnieuw in rust op ongeveer 4 meter van de sensor.

6.5 Verwerking

Volgens Doppler zou de gemeten frequentie hoger moeten zijn wanneer de geluidsbron de sensor nadert en kleiner wanneer de geluidsbron ervan weg beweegt. We kunnen dit ook vaststellen uit de gemeten waarden.

Als we het verloop van de waargenomen frequentie bekijken, zien we hoe de frequentie tijdens het opmeten van rechts naar links beweegt. Of anders gezegd van een grotere frequentie naar een lagere, met als midden 1000 Hz, de frequentie die de geluidsbron uitzendt.

We bekomen die frequentie maar op één moment. En dat is wanneer de snelheid van de geluidsgolven die naar de sensor gaan, loodrecht staan op de snelheid van de geluidsbron, ofwel wanneer de geluidsbron rakelings passeert bij de geluidsbron.

Download PDF

-Jerke Ghekiere
-Julian Ampe