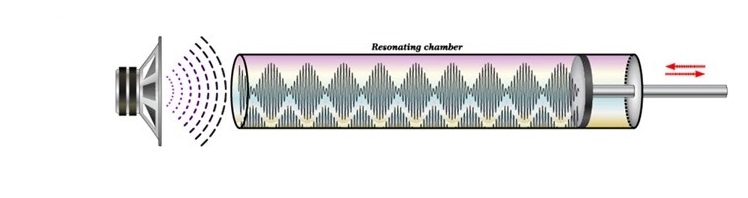
Ward en ik maken als GIP de proef van Kundt. Ons hoofddoel met deze proef is geluidsgolven te visualiseren met behulp van staande golven. We kunnen dan ook de afstand tussen twee knooppunten meten en de geluidssnelheid berekenen. Wij zouden dit proces ook graag zo veel mogelijk automatiseren. -Jerke Ghekiere