Theorie
Trillingen opwekken.
1. Inhoudstafel
1. Inhoudstafel2. Inleiding
3. August Kundt
4. Franz Melde
5. Besluit
Download PDF
2. Inleiding
Tegenwoordig zijn er enorm veel manieren om trillingen op te wekken. Maar hoe deden ze dat vroeger? In dit verslag toon ik aan hoe de geleerden vroeger trillingen genereerden bij hun experimenten.
3. August Kundt
August Kundt wilde de geluidssnelheid berekenen, daarvoor maakte hij staande golven in een buis. Om die geluidsgolven te genereren had hij een staaf, die was vastgeklemd in het midden. De ene kant zat dan in de buis, er ging dan ook een plaatje aan de staaf. Het plaatje raakte de buis niet. Deze proefopstelling is gekend als de proef van Kundt.
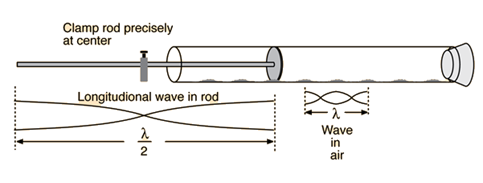
Wanneer hij van het midden van de staaf naar buiten toe wreef, met een doek waarop colofoniumpoeder werd gestrooid, dan ontstonden er longitudinale golven in de staaf. Het plaatje begon dan ook te trillen, waardoor de luchtdeeltjes in de buurt van het plaatje meetrilden. Hierdoor ontstonden geluidsgolven in de buis met een constante frequentie.
Als hij de zuiger verplaatste , dan ontstonden er bij bepaalde buislengtes staande golven in de buis. Door de staande golven vormde het lycopodiumpoeder in de buis hoopjes, dat zijn de knopen van de staande golven. Door het meten van de afstand tussen twee opeenvolgende knopen kun je de geluidssnelheid berekenen van het gas in de buis.
4. Franz Melde
Franz Melde zocht het verband tussen de kracht in een touw en de golfsnelheid van de golven in het touw. Hij maakte hiervoor een opstelling waarbij een touw werd opgespannen. Aan één kant was er een systeem om de kracht op het touw te verhogen of te verlagen. Aan de andere kant hing het touw vast aan een staafje van een stemvork. De staven van de stemvork stonden in deze opstelling parallel ten opzichte van het touw.

Wanneer de stemvork werd aangeslagen, trilde het touw mee met de stemvork. Bij bepaalde frequenties zal er dan een staande golf ontstaan in het touw. Wanneer hij dan de kracht veranderde op het touw veranderde de golfsnelheid en dus ook het aantal knopen en buiken. Op die manier vond hij uiteindelijk het verband tussen de kracht en de golfsnelheid op een touw.
5. Besluit
August Kundt en Franz Melde moesten trillingen genereren om hun experimenten uit te voeren. Maar vroeger bestonden de elektrische frequentiegenerators nog niet. Daarom maakten ze gebruik van de eigenfrequenties van materialen. August Kundt gebruikte een staaf om eigenfrequenties te aan te maken, terwijl Franz Melde een stemvork gebruikte.
-Jerke Ghekiere
Theorie
Golftheorie.
Voorwoord
Overal rondom ons is geluid, je kan er niet aan ontsnappen. ‘s Ochtens zingen vogels, overdag rijden er auto’s en zelfs ‘s nachts passeert er wel eens een trein. Maar wat is geluid precies en welke soorten geluid zijn er? In dit verslag zal ik deze vragen beantwoorden en ga ik nog een paar fenomenen rondom geluid onderzoeken.
1. Inhoudstafel
Voorwoord1. Inhoudstafel
2. Wat is geluid?
3. Soorten geluid
3.1 Niet-perdiodieke geluiden
3.2 Periodieke Geluiden
3.2.1 Zuivere tonen
4. Fenomenen
4.1 Zwevingen
4.2 Interferentie
Download PDF
2. Wat is geluid?
Geluid is een mechanische golf, bestaand uit deeltjes van een middenstof waarin de golf zich voortbeweegt. De deeltjes van een geluidsgolf bewegen steeds heen en weer. Maar de gemiddelde positie ervan blijft hetzelfde. De golf is dus niets anders dan een drukverschil dat zich voortplant in een elastisch medium. Doordat bij geluid de trilrichting van de deeltjes samenvalt met de voortplantingsrichting van de golf zelf, spreken we van een longitudinale golf.

3. Soorten Geluid
3.1 Niet-periodieke geluiden
Dit zijn geluiden waarvan er geen herhaling van golf is. Bijvoorbeeld bij het klappen van de handen (a) of het scheuren van een stukje papier (b).
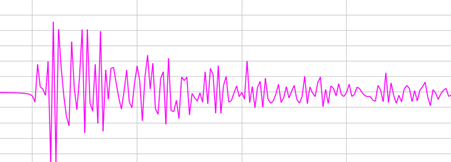
(a)
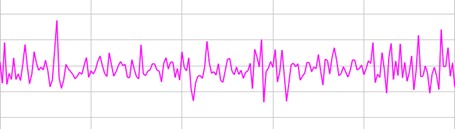
(b)
3.2 Periodieke geluiden
Bij periodieke geluiden is er wel een herhaling te zien in het golfpatroon. We noemen deze geluidsgolven tonen. De tijd tussen twee opeenvolgende herhalingen noemen we de periode. Als je het omgekeerde neemt van die periode heb je de frequentie van de geluidsgolf. In het voorbeeld onderaan wordt de klinker ‘A’ gezongen.
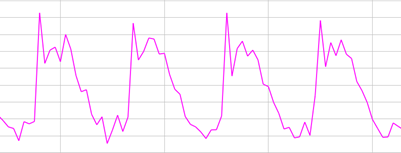
Nog een voorbeeld, maar met de klinker ‘ I ‘.
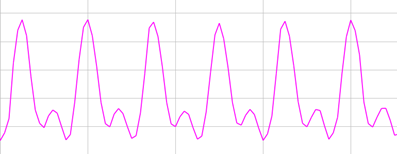
3.2.1 Zuivere tonen
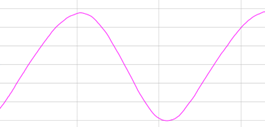
Wanneer we een stemvork aanslaan, zien we een sinusvorm. Deze tonen noemen we zuivere tonen, soms worden ze ook wel muzikale tonen genoemd.
4. Fenomenen
4.1 Zwevingen
We plaatsen twee stemvorken naast elkaar, de eigen frequentie van de eerste stemvork is 440 Hz. Die van de andere is ongeveer 443 Hz. We slaan ze allebei aan en meten de resultaten. Intussen horen we het geluid versterken en verzwakken. Op de grafiek zien we het gemeten geluid, dit is gelijk aan de som van de twee geluidsgolven gemaakt door de stemvorken.
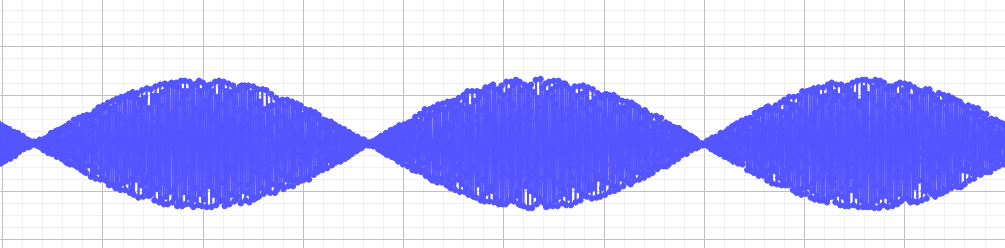
We kunnen op de grafiek de nieuwe functie zien, maar de amplitude verandert in functie van de tijd. Dit gebeurt ook met een constante frequentie. Als we de som van de twee oorspronkelijke sinusgolven maken, kunnen we dit ook aantonen.
\( y(t) = A*sin(2\pi[\frac{t}{T}-\frac{d}{\lambda}]) \)
(Deze formule werd opgesteld in het verslag “Golven” van Quinten Callewaert.)
We nemen de formules voor de twee golven en werken de som van de twee uit.
\(y_{1}(t) = A*sin(2\pi [\frac{t}{T}-\frac{d_{1}}{\lambda}])\)
\(y_{2}(t) = A*sin(2\pi [\frac{t}{T}-\frac{d_{2}}{\lambda}])\)
\(y(t) = y_{1}(t) + y_{2}(t)\)
\(y(t) = A*sin(2\pi [\frac{t}{T}-\frac{d_{1}}{\lambda}]) + A*sin(2\pi [\frac{t}{T}-\frac{d_{2}}{\lambda}])\)
\(y(t) = A[sin(2\pi [\frac{t}{T}-\frac{d_{1}}{\lambda}]) + sin(2\pi [\frac{t}{T}-\frac{d_{2}}{\lambda}])]\)
\(y(t) = 2A[sin(\frac{2\pi(\frac{t}{T}-\frac{d_{1}}{\lambda}+[\frac{t}{T}-\frac{d_{2}}{\lambda}])}{2})*cos(\frac{2\pi(\frac{t}{T}-\frac{d_{1}}{\lambda}-[\frac{t}{T}-\frac{d_{2}}{\lambda}])}{2})]\)
\(y(t) = 2Acos[\pi(\frac{d_{2}-d_{1}}{\lambda})]*sin[\pi(\frac{2t}{T}-\frac{d_{1}+d_{2}}{\lambda})]\)
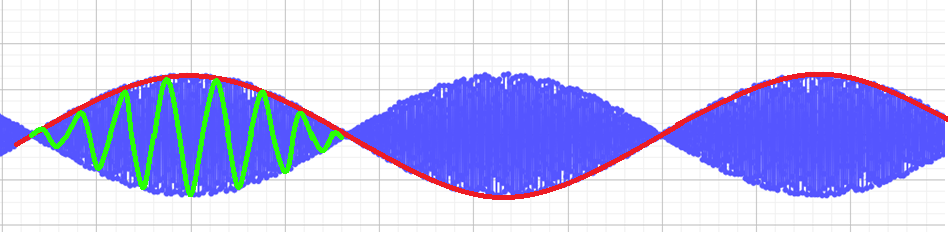
We splitsen deze functie op in \(sin[\pi(\frac{2t}{T}-\frac{d_{1}+d_{2}}{\lambda})]\) en \(2Acos[\pi(\frac{d_{2}-d_{1}}{\lambda})]\).
\(sin[\pi(\frac{2t}{T}-\frac{d_{1}+d_{2}}{\lambda})]\) zien we als de frequentie van de functie. Dan blijft \(2Acos[\pi(\frac{d_{2}-d_{1}}{\lambda})]\) nog over, we zien dit als de amplitude. De cosinus heeft een bereik tussen [-1, 1] dus de amplitude ligt tussen [-2A, 2A]. Dit is ook te zien op de grafiek.
4.2 Interferentie
Twee geluidsbronnen staan twee meter van elkaar vandaan. Beide geluidsbronnen sturen een toon met een frequentie van 470 Hz. Hierdoor ontstaan er twee golven, ze bewegen in tegenovergestelde richting en hebben een faseverschil van 180°. De twee geluidsgolven creëren een staande golf met knopen en buiken. Dit zijn plaatsen waar er maximale beweging is van luchtdeeltjes (buiken) en plaatsen met minimale beweging van luchtdeeltjes (knopen). We verplaatsen de geluidssensor van links naar rechts tussen de geluidsbronnen. We zien op bepaalde plaatsen een grotere sinusgolf en op andere plaatsen zien we een uitdoving.
Eén geluidsbron met sinusgolf van 470 Hz:
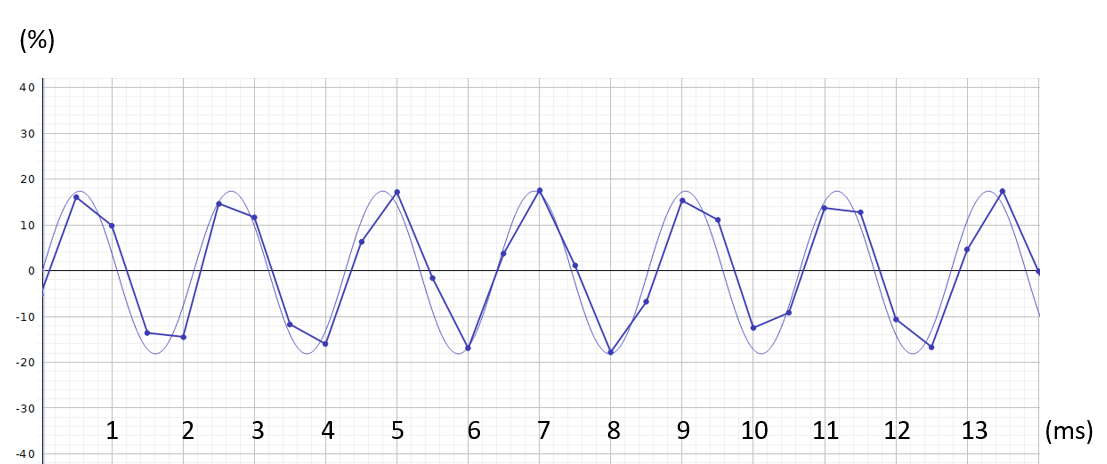
Wat we meten bij een buik van de staande golf:
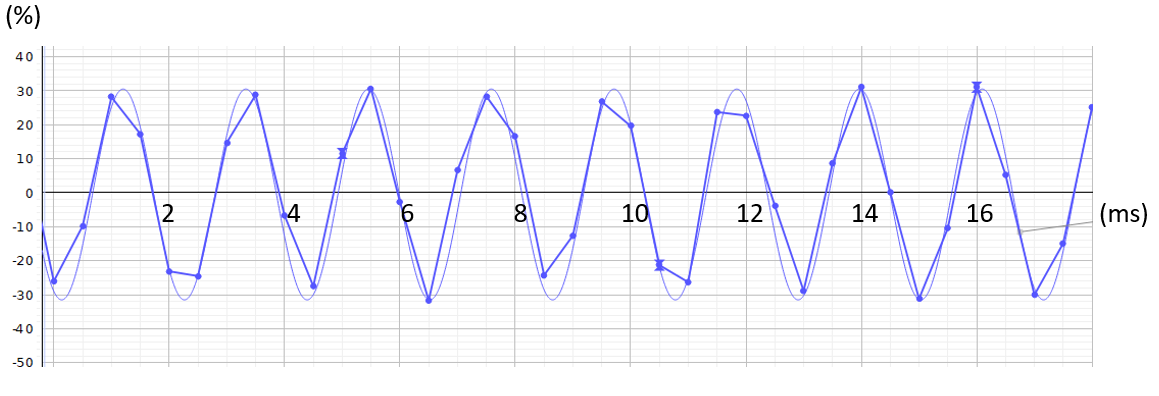
Wat we meten bij een knoop van de staande golf:
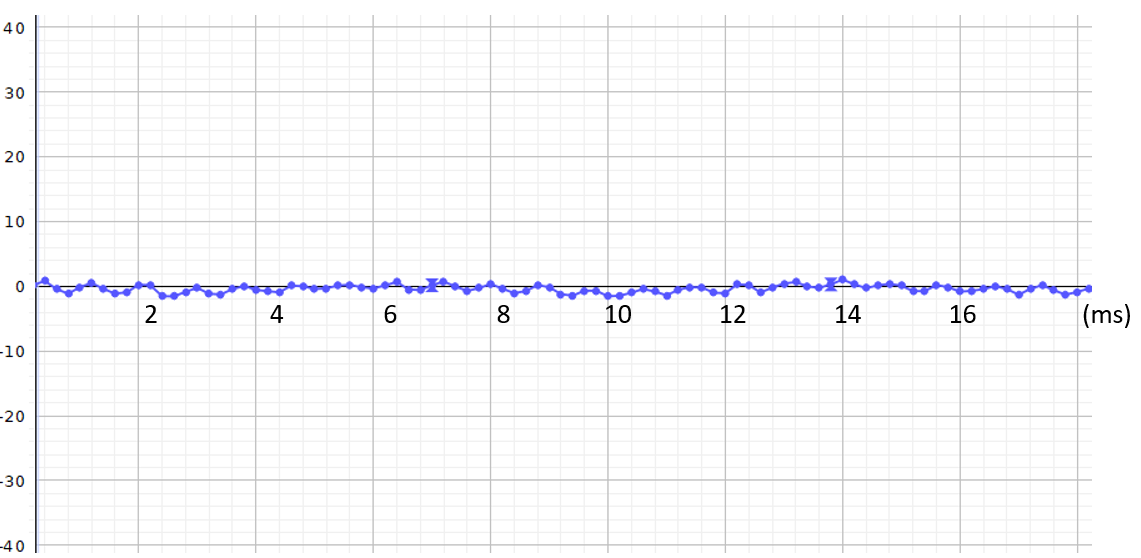
Op de grafiek zien we dat er geen duidelijke sinusvorm is, de twee golven doven elkaar uit. We merken ook dat de frequentie gelijk blijft en alleen de amplitude verdubbelt.
Theorie
Staande golven.